目的

  • 以拒绝率或拒绝可能性描述 QC 程序的性能特征
  • 区分假拒绝率与误差检出率
  • 比较常用 QC 程序的预期拒绝特性
  • 应用功效函数图得到不同 QC 程序的假拒绝和误差检出信息

功效曲线

问题

  • 2s 控制限的高拒绝次数的原因是什么?
  • N=2 时, 12s 规则预期的假拒绝率是多少?
  • N=1 和 2 时, 13s规则预期的假拒绝率是多少？
  • 在 12s 和 13s 中，哪一个规则具有更好的出率?
  • 3s 控制限的拒绝次数为什么会下降?

QC 拒绝的可能性

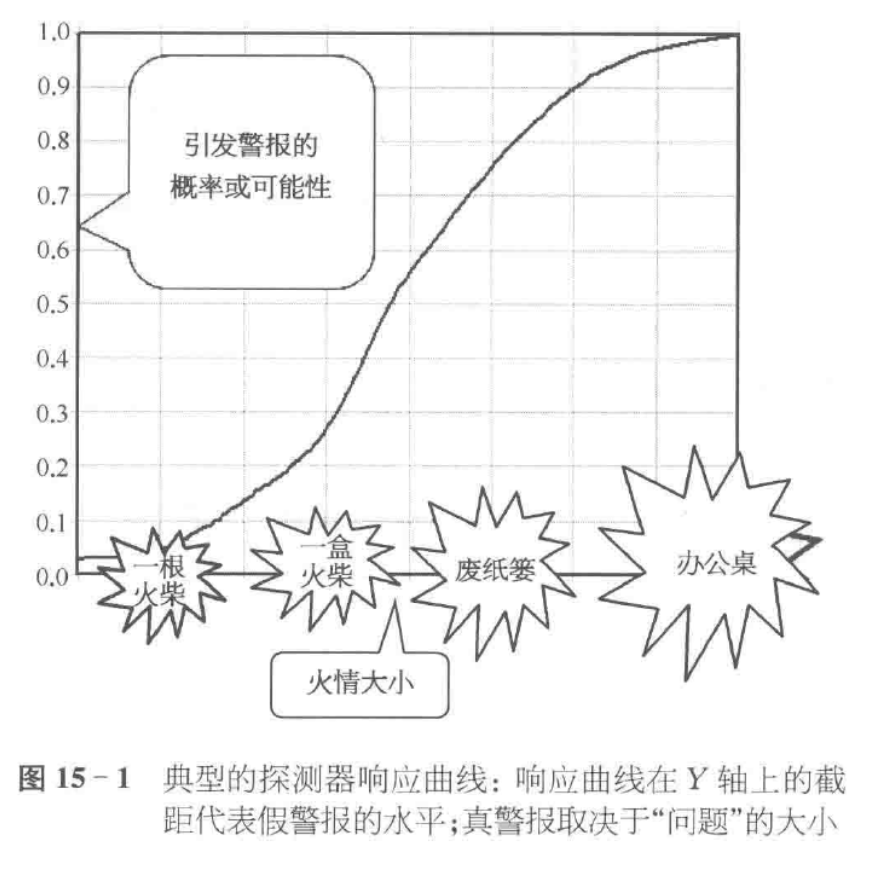
火警报警器的案例：

误报警

我们期望检出某个分析问题的可能性取决于发生误差的大小、用于监控方法性能的控制品的个数，以及所用统计规则的灵敏度。我们需要对医学上的重要误差有较高的误差检出可能性或概率，但又不希望在方法正常运行时被假警报所打扰。

QC 拒绝特性

描述探测器性能的专用术语是真警报的频率和假警报的频率；对于 QC 程序，这些特性被分别称作误差检出率和假拒绝率。

  • 误差检出率， Ped 是在检测程序稳定的不精密度之外，对发生了外来误差的某个分析批被拒绝的概率。理想情况下， Ped 应是 1. 00， 意即检出某误差的可能性是 100％。实际 Ped 的设计目标为 0. 90， 意即检出某个分析问题的可能性是 90％。
  • 假拒绝率， Pfr 是在检测程序稳定的不精密度之外，没有发生外来误差的某个分析批被拒绝的概率。理想情况下， Ped 应当是 0. 00， 即提供假拒绝的可能性是 0。实际工作中， Ped 的设计目标为 5％或更低，意即假拒绝的可能性仅为 5％或更低。

功效函数图

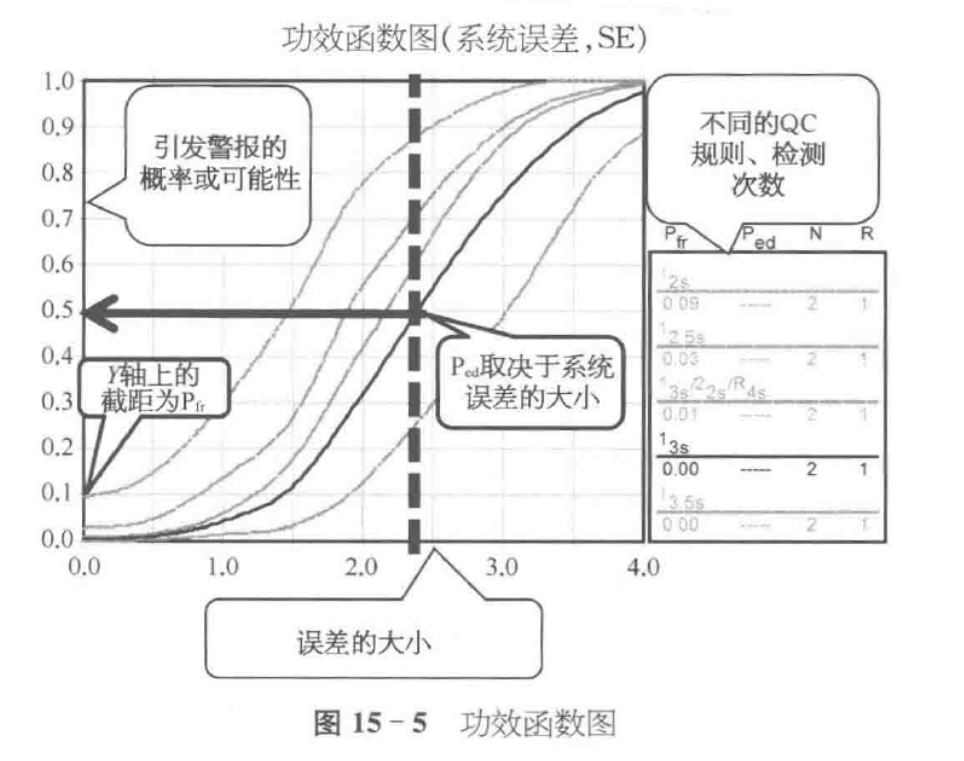
每条线或功效曲线，代表图上右侧图例中列出的某种控制规则与控制检测次数（N)组合的拒绝概率。功效曲线在 Y 轴上的截距为每个 QC 程序的假拒绝率。误差检出率取决于发生误差的大小。 例如，最上方的功效曲线代表 N=2 时 12 控制规则的性能，即设置了 2SD 控制限的 Levey – Jennings 控制图及每个分析批做 2 次控制检测。其假拒绝率大约为 0. 09 或 9％， 如该条曲线在 Y 轴上的截距所示。 通过比较可知，在 N=2 时 13s 控制规则(从下往上数第二条曲线）的假拒绝率非常低，接近于 0。

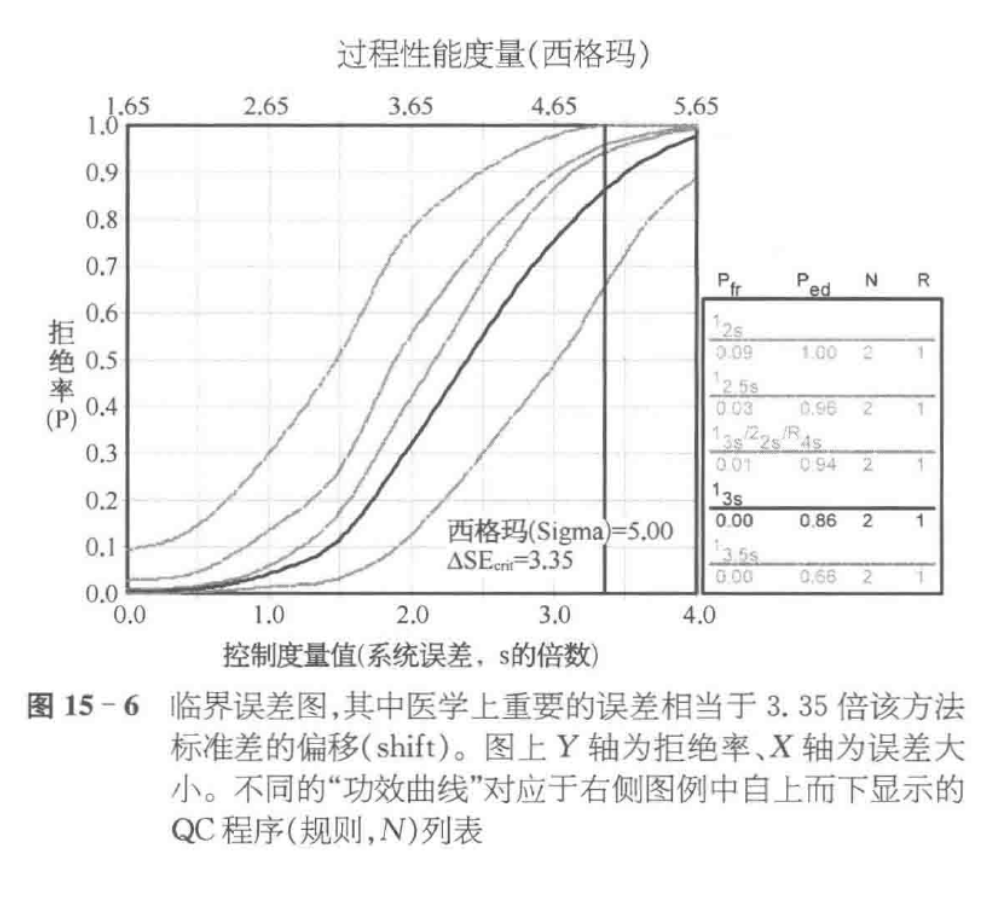
临界误差图

显示临界误差的功效函数图也称之为临界误差图。可通过如下公式计算需要检出的临界系统误差($\Delta SE_{crit}$):

$$\Delta SE_{crit}=[(TE_{a} -bias_{meas})/S_{meas} ]—1. 65$$

  • TEa 是该项目以总允许误差形式表示的质量要求。
  • biasmeas 是观测到的该方法的不准确度（即检测偏移）。
  • Smeas 是观测到的该方法的不精密度。

例如，根据 CLIA PT 的可接受性能标准，某种胆固醇检测方法的总误差要求在 10％以内。

误差检出

随之降低。对检出系统误差最敏感的规则是 22s、2/32s、31s、41s、6x及8x ；对随机误差最敏感的规则是 13s、12.5s 及 R4s 规则。使用 13s 和 12.5s 单规则程序且 N 为 1～4 时，其灵敏度已足以监控当下精密度极高的自动化系统的检测性能。对于那些“较早”年代的仪器和手工方法，可能依然有必要使用由 13s、22s 或 2/32s 、R4s、31s 或 41s、6x 及 8x ， 等规则组成的多规则程序。

功效函数图可提供更多关于 QC 程序拒绝特性的量化信息，反映了作为误差检出系统功用之一的拒绝概率。为阐述系统误差和随机误差的检出，需要分别提供对应的功效函数图。

拒绝特性的总结

表 15–1 不同控制规则对不同误差的响应

改善 QC 性能的途径基于不同控制规则的预期响应，如上表的总结，选择一个 QC 程序的通用做法如下：

  • 排除那些假拒绝率很高的控制规则。
  • 选择一个规则组合，其中至少各有一个规则分别响应随机误差和系统误差。
  • 评估该组合规则的拒绝率。
  • 选择总的控制检测次数以提供期望的误差检出率。 当实验室规定了某项目要求的质量，确定了方法的不精密度与不准确度，并考虑了目标控制规则与 N 组合的特定功效曲线，就有可能进行更为量化的质量设计与策划流程。

如何选择 QC 程序

需要应用一个定量策划流程来为本实验室的项目和方法选择最佳的 QC 程序。这个 QC 设计与策划流程将基于项目要求的质量、实验室方法实际的不精密度和不准确度，以及 QC 程序已知的拒绝特性，帮助实验室选择控制规则和控制检测次数。