目标

  • 建立一个 Levey-Jennings 图
  • 把控制数据绘制到 Levey - Jennings 图上
  • 用单一规则解释控制结果
  • 比较不同控制规则的拒绝次数

应用

初始计算

本章举例说明如何为设置控制图进行初始计算，建立 Levey-Jennings 图，绘制控制值和解释结果。 这堂课假设实验室已经选定了控制品，并在 10 天内进行了至少 20 次检测。

2 个控制品每天检测 1 次，共 20 天。根据这些数据计算均值和标准差，用于设置控制图。

计算控制品的均值和标准差。

总体或样本的平均值。总体的平均值用 $$ μ $$ 来表示。样本的平均值用 $$\bar x$$ 来表示。

$$ \bar {x} = \frac {1} {n}\left (\sum\limits_{i = 1}^n{x_i}\right) = \frac {x_1 + X _2 + \cdots + x_n}{n} $$

excel 计算公式：

$$ \bar x = average(x_1:x_n) $$

标准差

衡量数据分散程度的一个指标。一般用σ表示总体，用 s 或$$ \hat σ $$表示样本。

总体标准差：

$$ σ = \sqrt\frac {\sum\limits_ {i = 1} ^ n {(X_i - \mu)}^2}{N} $$

样本标准差：

$$ S = \hat \sigma = \sqrt{\frac {\sum\limits_{i=1} ^n (X_i - \overline X)^2} {N-1} } $$

实施 QC 程序

每分析批对这两个控制品进行一次检测，即每分析批合计提供 2 个控制品检测结果，再根据 12s 或 13s 规则判断控制状态。

定义控制规则

  • 12s 是设定控制限为均值±2s 的控制规则。

    常用于 Levey- Jennings 图。在许多实验室只要个控制结果超出 2s 控制限时就拒绝该分析批。

  • 13s 是设定控制限为均值＋3s 与均值一 3s 的控制规则。

    常用于 Levey - Jennings 图。当一个控制检测结果超值＋3s 或均值－3s 时，该分析批被拒绝。

12s 规则在当下被广泛使用。该规则虽然提供了较高的误差检出率，但也带来了非常高的假性拒绝率。

13s 规则提供了另一个可选的 QC 程序，具有很低的假性拒绝率，但误差检出率也低。本练习将展示如何应用这两个 QC 程序，并让读者体会到这两者在性能上的差异。

计算控制限

$$ \bar x \pm 2 \sigma \ \bar x \pm 3 \sigma $$

准备控制图

  1. 图表本体，20 X 20 格
  2. 图表标注
  3. X 轴的刻度与标注
  4. Y 轴的刻度与标注
  5. 绘制均值与控制限线

使用控制图

控制图设定后，就可以开始把日常工作收集的新的控制数据绘制到控制图上。重点在于：对一个稳定的检测过程，新的控制检测结果应与以往控制检测结果的分布相同。 因此看到一个超出 2s 控制限的控制值是少有的，而看到一个超出 3s 控制限的控制值更为稀罕。若该方法不稳定和存在某些问题，此时出现超出控制限的控制值的可能性大大增加。 因此，当控制值落在预期分布范围内时，该批判断为“在控”, 接受这些结果并报告患者检测结果。 当控制值落在预期分布范围之外时，该批判断为“失控”, 拒绝这些结果且不得报告患者检测结果。

绘制控制值

image-20220620155649512

解释控制结果

  1. 使用 12s 和 13s 规则解释和控制结果
  2. 应用不同的控制规则将出现不同的情况

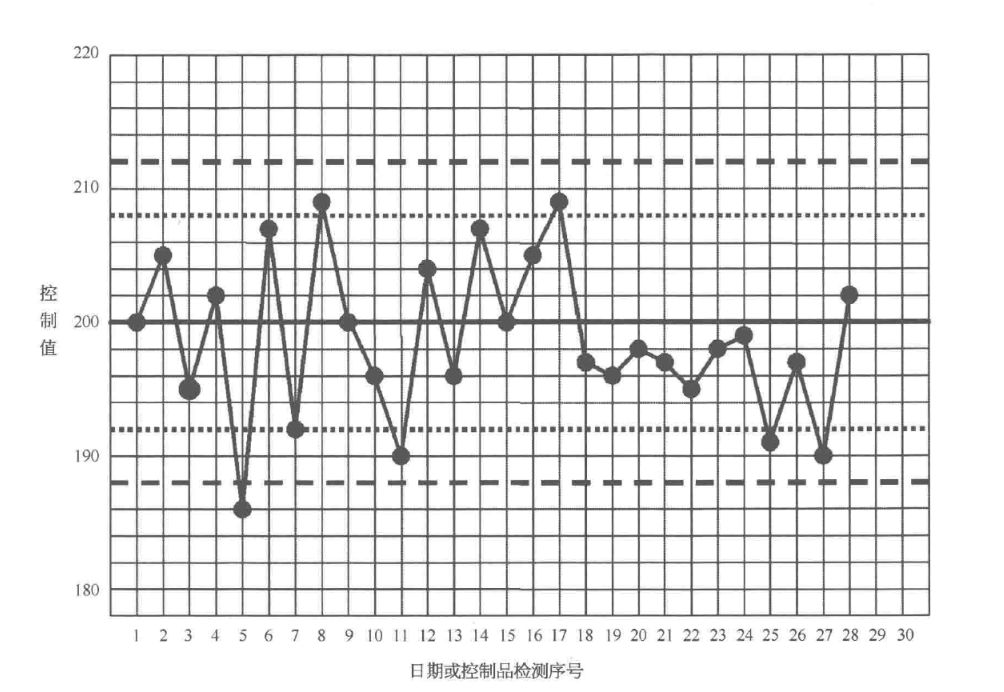
image-20220620155918029

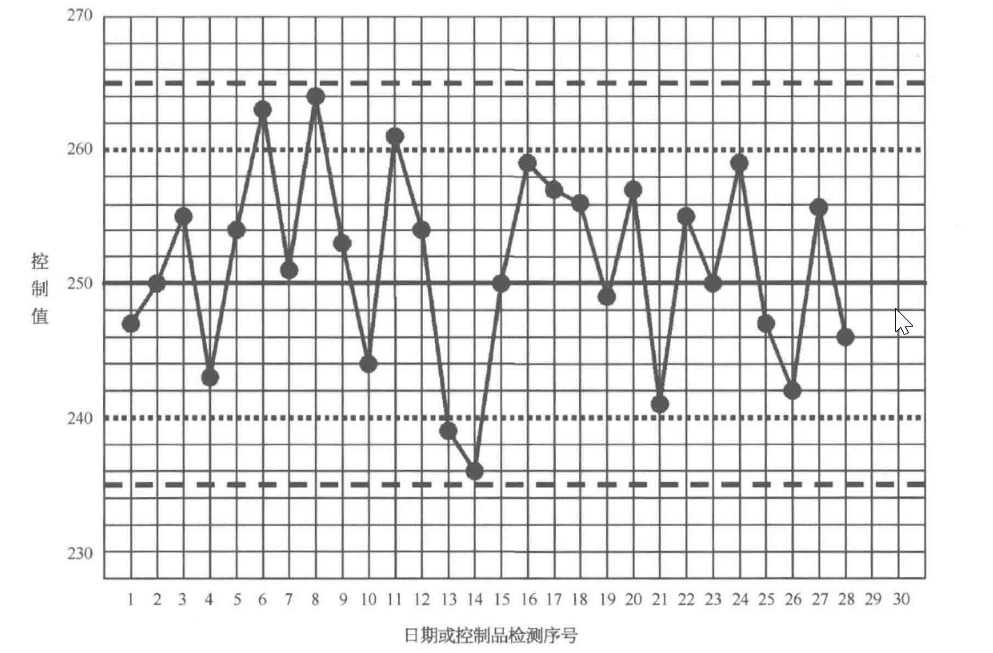
image-20220620155944416

Levey - Jennings QC 实践结果

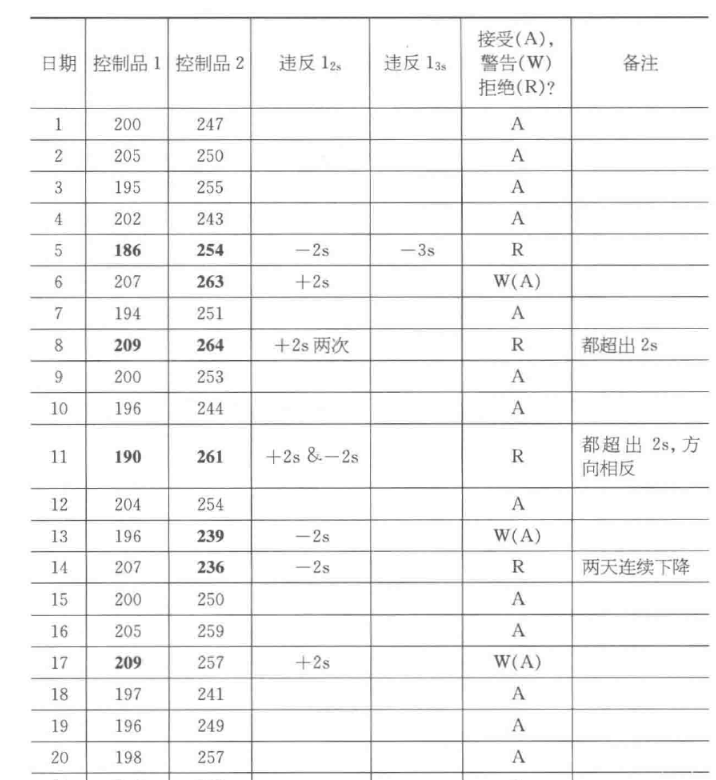
image-20220620160023944