可报告范围：可靠且可以报告的最高和最低检测结果。

  • 检验厂商对范围的声明，尤其是对于假设呈线性，且使用两点校准的方法。

厂商通常为校准其方法提供了指导和校准品。方法的校准周期可以是每分析批，或每天、每周、每月甚至更长的周期，或仅在启用新批号试剂之时，取决于厂商的方法稳定性文件。如果校准的周期很长，实验室可能需要定期验证校准是否正确，这一职能在 CLIA 最终法规中称为“校准验证”。

校准是一个程序，确定分析方法产生的信号与报告的检测结果间的关系。对于不能产生线性响应的方法（如免疫分析方法），要求“多点校准”，常需要检测 3~5（或更多）个校准液及运用曲线拟合常规建立校准函数。

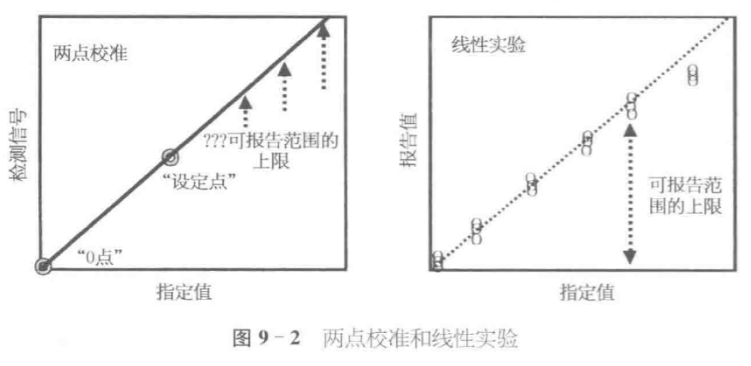
两点校准和线性实验

进行的实验经常称为“线性实验”，尽管技术上并不要求方法提供线性响应，除非使用了两点校准。虽然 CLIA 使用了“可报告范围”，而不是“线性范围”，但通常仍然将此范围作为方法的“线性范围”“分析范围”或“工作范围”。

术语定义

校准：

检测并调整仪器或检测系统的过程，以建立检测响应与检测程序检测物质的浓度或含量的相互关系。

校准验证：

指采用与检测患者样品相同的方式，检测已知浓度的物质，证实在整个患者检测结果的可报告范围内仪器或检测系统的校准。请注意“校准验证”与“可报告范围”的关系，后者在 CLIA 最终法规中的定义如下：

可报告范围：

指检测结果分布的范围，在该范围内，实验室可建立或验证仪器或检测系统检测响应的准确性。

美国病理学家协会 (CAP) 使用了如下不同术语：

分析测量范围 (AMR)：

即方法可直接对未经任何稀释、浓缩或其他非常规检测流程前处理的标本的检测，得到的分析物浓度范围。

临床可报告范围 (CRR)：

指在允许对标本进行稀释、浓缩或其他前处理以拓展直接分析测量范围的前提下，方法可以检测的分析物浓度范围。

原则上，AMR 相当于 CLIA 的可报告范围，而 CRR 提供了更多实用信息，考虑了方法的检出限和/或通过稀释患者标本验证的程序拓展了 AMR。

有些指南，如 CLSI 的 EP6 规程为评价分析方法的线性推荐了更复杂的统计计算：

EP06Ed2 | Evaluation of Linearity of Quantitative Measurement Procedures, 2nd Edition (clsi.org)

查看线性图评估可报告范围。此时可能会手工绘制通过数据点线性部分的最佳直线，也绘制连接各点的折线，与最佳直线比较，或对线性范围内的点进行统计拟合回归线。通常认为“目视”评估已可确定可报告范围，即手工绘制拟合系列最低点的最佳直线。

水平数

CLSI 推荐至少检测 4 个（最好 5 个）不同浓度水平 3,5 个以上也可以，尤其需要最大的可报告范围的上限时。但我们发现 5 个水平既便于操作，又基本可以满足需求。

重复检测的次数

CLSI 推荐对每个标本或混合样品重复检测 4 次。实际工作中，我们发现通常重复检测 3 次即可，意即初始的高浓度和低浓度混合样品也同样重复检测 3 次。

数据分析

以检测值的均值为 y, 以定值、相对值或稀释因子为 x, 绘制散点图。接下来，先绘制各相邻点连线通过整个分析范围，再手工绘制通过最多数据点的最佳直线，并确保直线贴近较低点、较低标准或稀释值。在直线不贴近的数据点浓度处，评估非线性引起的系统误差。将此系统误差加上该浓度处预期的随机误差 (2SD) 与该项目的允许总误差比较。

可报告范围与校准验证

根据 CLIA 的定义，校准验证是指以与检测患者样品相同的方式检测已知浓度的物质，在整个患者检测结果的可报告范围内对仪器或检测系统的校准进行验证。那些校准频率较低的检测系统，必须至少每 6 个月进行一次校准验证：且当彻底更换了试剂、更换了关键零部件、进行了重大保养或某个无法纠正的 QC 问题证明检测结果发生漂移时，应增加校准验证的频率。

校准验证实验看上去与可报告范围实验很相以，主要差别在于前者必须使用提供了定值的物质。这些物质可以是厂商或试剂供应商提供的某个特定校准系列，或像患者样品一样作为未知值样品进行检测的校准品，或定值的控制品，或提供了已知值的能力验证样品，甚至具有检测值的患者样品。CLIA 条款中关于检测类似患者标本物质的规定，不应视为对实验设计的限制。重复检测样品，将可提供因校准可能引入系统误差的更佳信息。

数据分析程序应当确定观测值与定值之间的差异，然后将这些差异与实验室制定的可接受标准进行比较。如果进行了重复检测且确定了这些结果的均值，则与本章介绍的可报告范围的数据分析方法相以。如果只进行了单次检测，则可将观测的差值与 CLIA 规定的允许总误差直接进行比较。

问题：

  • 确认可报告范围通常需要检测几个浓度水平的材料？

  • 准备这一系列材料的实用方法是什么？

  • 通常进行几次重复检测？

  • 如何分析数据评估可报告范围？

  • 如何分析数据评估线性？